How to Draw a Circle (Midpoint and Bresenham's Algorithm)

With trigonometry functions such as sine and cosine, it is very easy to compute for the value of x and y for any given radius and teta.
px = cx + radius * cosine(0);
py = cy + radius * sine(0);
for (teta = 1; teta <= 360; ++teta)
{
px = cx + radius * cosine(teta);
py = cy + radius * sine(teta);
line(px, py, x, y);
px = x;
py = y;
}
We've all learned this from highschool trigonometry class and it will not be tacked in this article. However, drawing a circle using these functions requires the usage of floating-point numbers which is slow, not to mention the typecasting from floating-point to integers as plotting a pixel requires integral datatype. And finally, the big turnoff of this script is using the line segment function to connect the dots.
You can improve the above code by reducing the computational complexity by dividing the circle to quadrants, octants, or whatever.
Midpoint Circle Algorithm
Understanding the algorithm starts with the circle formula
- x2 + y2 = r2
For simplicity of computation, we don't have to compute for the x and y of the entire circle given r. We can divide it into quadrants, octants, or whatever suits your preference. In our case, we will divide the circle by 8, which means we only need to compute 0 degrees to 45 degrees. Also to further simplify, our circle will be centered at coordinates (0, 0).
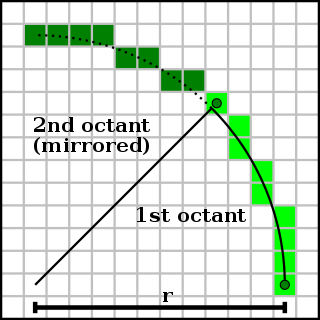
Notice on the first octant, that y continually increases while xi+1 is either on the same position as xi or xi - 1. We'll consider y as fast direction and x as the slow direction in this case. This means that x decreases by some factor of the circle. But how do we get x based on the previous values of x and y?
For each point in the circle, the following formula holds, where i is the iteration starting from 0.
- x2i + y2i = r2
To get the x we can rearrange the above to:
- x2i = r2 - y2i, the next point would be x2i+1 = r2 - y2i+1
Since y is the fast direction, y increases for every iteration in the first octant, hence:
- y2i+1 = (yi + 1)2
Let's substitute this to x2i+1
- x2i+1 = r2 - (yi + 1)2
- x2i+1 = r2 - y2i - 2yi - 1, we can simplify by the computation by replacing r2 - y2i by x2i, which gives us:
- x2i+1 = x2i - 2yi - 1
- xi+1 = √[ x2i - 2yi - 1 ]
Now that we a formula of x that is dependent on the previous value, we can start writing our program. The following is written in C/C++ and SDL (actually all other programs below are written using the same language and framework):
void drawCircle1(SDL_Surface* surface, Sint32 cx, Sint32 cy, Uint32 r, Uint32 rgba)
{
Sint32 x, x2, xn, y, xsurface, ysurface;
// Center position the pointer
Uint32* pixels = (Uint32*)surface->pixels + cx + (cy * surface->w);
// Starts plotting (0, 0)
x2 = r * r;
x = sqrt(x2);
y = 0;
while (x > y)
{
xn = (x2 - (2 * y) - 1);
x = sqrt(x2);
xsurface = x * surface->w;
ysurface = y * surface->w;
// First Octant
*(pixels + x - (ysurface)) = rgba;
// The rest of the octants
*(pixels + y - (xsurface)) = rgba;
*(pixels - y - (xsurface)) = rgba;
*(pixels - x - (ysurface)) = rgba;
*(pixels + x + (ysurface)) = rgba;
*(pixels + y + (xsurface)) = rgba;
*(pixels - y + (xsurface)) = rgba;
*(pixels - x + (ysurface)) = rgba;
x2 = xn;
++y;
}
}
Output:
It is important to take note that the upper left coordinates of the screen is (0, 0), and x and y increase as we move southeastwards, therefore adjustments are made to plot the first octant in the cartesian plane. The rest of the octants are computed accordingly.
Although the above script works, it could have been more elegant if floating-point computation such as square root, and typecasting have been eliminated.
Bresenham's Derivation of Drawing a Circle
To completely remove the floating-point computation, we need to start with the so-called Radius Error (RE). RE is can be thought of as a deviation of computation of points. If we've detected a deviation then we need to do correction in x position (assuming we're working on the first octant). If we're starting again with the first octant at (r, 0), we can say that REi, where i = 0, is zero (0), because we're sure that x = r and y = 0 at this point, and we can plot these two values using integral data type, hence we can write:
- RE(xi, yi) = | x2i + y2i - r2 | = 0, where | | denotes absolute value.
when i = 0, on first octant,
- RE(xi, yi) = | x2i + 0 - r2 | = 0
Just like the Midpoint algorithm, and since we're starting with the first octant, we know that y is the fast direction and x is the slower. Therefore, as y increments, x can either stay in the same position or decrement by one (1). To give a solution to this, we define a decision statement to determine if we need to retain the value of x or decrement the value of x as y increases.
RE(xi - 1, yi + 1) < RE(xi, yi + 1), if the value of the left hand side is less than the right, then we plot RE(xi - 1, yi + 1), otherwise RE(xi, yi + 1).
To start the determination, let's substitute the value of RE. This gives us the following equation:
- = | (xi - 1)2 + (yi+ 1)2 - r2 | < | xi2 + (yi + 1)2 - r2 |
Expanding the equation gives us
- = | (x2i - 2xi + 1) + (y2i + 2yi + 1) - r2 | < | xi2 + (y2i + 2yi + 1) - r2 |
Rearranging will give us
- = | x2i - 2xi + 1 + y2i + 2yi + 1 - r2 | < | xi2 + y2i + 2yi + 1 - r2 |
- = | x2i + y2i - r2 + 2yi + 1 + 1 - 2xi | < | xi2 + y2i - r2 + 2yi + 1 |
- = | (x2i + y2i - r2 + 2yi + 1) + (1 - 2xi) | < | (xi2 + y2i - r2 + 2yi + 1) |
Since absolute function | | requires additional library, we replace it by squaring both sides of the equation.
- = [ (x2i + y2i - r2 + 2yi + 1) + (1 - 2xi) ]2 < [ (xi2 + y2i - r2 + 2yi + 1) ]2
Expanding the left hand side of the equation gives us:
- = (x2i + y2i - r2 + 2yi + 1)2 + 2(1 - 2xi)(x2i + y2i - r2 + 2yi + 1) + (1 - 2xi)2
- < (xi2 + y2i - r2 + 2yi + 1)2
Canceling out (xi2 + y2i - r2 + 2yi + 1)2
- = 2(1 - 2xi)(x2i + y2i - r2 + 2yi + 1) + (1 - 2xi)2 < 0
And since we know that x > 0 in the first octant, the term (1 - 2xi) < 0, dividing both sides will cancel out the negative, giving us
- (a) = 2 [ x2i + y2i - r2 + 2yi + 1 ]+ (1 - 2xi) > 0
- (b) or simply = 2 [ RE (xi, yi) + Ychange ] + Xchange > 0
If the statement is true, then we decrement the value of x, otherwise, x stays at the same position.
Consider statement (a), to translate the decision statement to program, we write:
void drawCircle2(SDL_Surface* surface, Sint32 cx, Sint32 cy, Sint32 r, Uint32 rgba)
{
Sint32 x, x2, xn, y, y2, r2, re, xsurface, ysurface;
// Center position the pointer
Uint32* pixels = (Uint32*)surface->pixels + cx + (cy * surface->w);
r2 = r * r;
x = r;
x2 = x * x;
y = 0;
while (x > y)
{
xsurface = x * surface->w;
ysurface = y * surface->w;
y2 = y * y;
re = x2 + y2 - r2;
if ((2 * re) + (4 * y + 2) + (1 - (2 * x)) > 0)
{
--x;
x2 = x * x;
}
// First Octant
*(pixels + x - (ysurface)) = rgba;
// The rest of the octants
*(pixels + y - (xsurface)) = rgba;
*(pixels - y - (xsurface)) = rgba;
*(pixels - x - (ysurface)) = rgba;
*(pixels + x + (ysurface)) = rgba;
*(pixels + y + (xsurface)) = rgba;
*(pixels - y + (xsurface)) = rgba;
*(pixels - x + (ysurface)) = rgba;
++y;
}
}
The above script can still be further improved by eliminating multiplication in the script by the following:
- bit shifting to the left one time multiplies the integer by 2, bit shifting to the left two times multiples the integer by 4 (refer to drawCircle3() function in attached .cpp file)
- Consider the 3 quantities in the equation at close inspection and determine their values at different values of xi and yi. Let's find a way to do it iteratively to reduce the computational complexity (removal of squares - multiplication).
- RE (xi, yi) = x2i + y2i - r2
- Ychange = 2yi + 1
- Xchange = 1 - 2xi
- Since we're starting with x =r, y = 0, and RE (x0, y0) = 0, let's set RE initially to 0, Ychange = 1, and Xchange = 1 - (2 * r);
- We increment RE byYchange every iteration since, y is in the fast direction.
- We increment Ychange by 2 based on the formula.
- We compare ( 2 x RE + Xchange > 0), if true then that's the time we decrement x and increment RE by Xchange and increment Xchange y 2 based on the formula.
The complete program of plotting a circle using integer arithmetic is shown below:
void drawCircle4(SDL_Surface* surface, Sint32 cx, Sint32 cy, Sint32 r, Uint32 rgba)
{
Sint32 x, y, xsurface, ysurface;
Sint32 xchange, ychange, re;
// Center position the pointer
Uint32* pixels = (Uint32*)surface->pixels + cx + (cy * surface->w);
x = r;
y = 0;
xsurface = x * surface->w;
ysurface = y * surface->w;
xchange = 1 - (r << 1);
ychange = 1;
re = 0;
while (x > y)
{
// First Octant
*(pixels + x - (ysurface)) = rgba;
// The rest of the octants
*(pixels + y - (xsurface)) = rgba;
*(pixels - y - (xsurface)) = rgba;
*(pixels - x - (ysurface)) = rgba;
*(pixels + x + (ysurface)) = rgba;
*(pixels + y + (xsurface)) = rgba;
*(pixels - y + (xsurface)) = rgba;
*(pixels - x + (ysurface)) = rgba;
++y;
re += ychange;
ychange += 2;
if ((re << 1) + xchange > 0)
{
--x;
xsurface -= surface->w;
re += xchange;
xchange += 2;
}
ysurface += surface->w;
}
}
So there you go, an elegant solution (with an explanation of the derivation) as to how you can draw a circle efficiently. Feel free to play around with the codes and import it to your programming language of choice.


