How to Build a Sierpinski Triangle (Chaos Game)
Today is Throwback Thursday and so I decided to create a simple graphic script using QBASIC - the first programming language I fell in love with in the 90s.
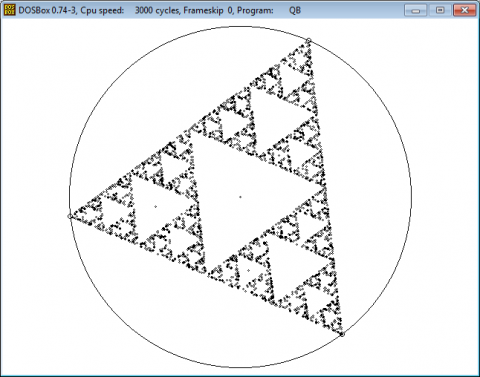
Sierpinski Triangle is a fractal equilateral triangle (60 degrees on each angle with equal length of sides) subdivided recursively into smaller triangles as shown in the figure above.
Although the pattern can be easily created using recursion, our demonstration uses the chaos game approach to construct the triangle.
To construct the triangle thru Chaos Game, one must do the following:
- Assign three(3) vertex points on the screen (Preferably an equilateral triangle).
- Start with a random coordinate within the boundary of the vertex points.
- Randomly select any of the vertices.
- Mark the midsection point of the line between your starting coordinate and your randomly selected vertex. This marked section will be your new starting point.
- Repeat step 3 for a number of times
Here's the video of the script output and a variation of it at four (4) edges.
Chaos Game method is exciting and at the same time disturbing in the sense that we can get order and beauty thru randomness. It's hard to imagine at first how the method avoids the spaces even if you start in the middle. But as you realized, this is the effect of vertex points and marking the point between the last point and the vertex.
Other fractals can be created by adjusting the number of vertices (let's say to 4) and restricting the randomness of selected edges. But I'll leave it up to you to explore. Download the code and adjust as necessary.
Here's the full script in QBASIC:
SCREEN 12
RANDOMIZE TIMER
'Parameters
'
sw = 640 'max screen width in pixels
sh = 480 'max screen height in pixels
cx = sw / 2 'center of fractal in X dimension
cy = sh / 2 'center of fractal in Y dimension
cr = 230 'scaled size of fractal in half of pixels from the center
edges = 3 'choose 3 if you want triangle, choose 4 for the square
circuit = 3.1416 * 2 'circumference of circle in 1 unit
circuiti = circuit / edges 'equally divide the circle with the number of edges
maxdots = 3500 'the more dots, the more clearer the fractal will be
wp = 2 'way point defaults to 2 (will be divided by2), try to experiment with other values (1 - 2) i.e. 1.5
allowrepeatedEdges = 1 '1 or 0, choose 0 if you want the square fractal
thickdots = 1 'size of the dots, 0.5 = dot, 1, 2, 3....
repeatdraw = 1 'no of times to repeat the fractal
backcolor = 15 'background color
dotcolor = 0 '0 - 15, 16 multicolor
''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''
TYPE vertices
x AS INTEGER
y AS INTEGER
END TYPE
DIM v(edges) AS vertices
FOR repeatdraw = repeatdraw TO 1 STEP -1
'
' Set background color
'
LINE (0, 0)-STEP(sw - 1, sh - 1), backcolor, BF
CIRCLE (cx, cy), cr, dotcolor
'
' Set and draw the vertices
'
circuitr = RND * circuit
FOR i = 1 TO edges
v(i).x = cx + (COS(circuitr) * cr)
v(i).y = cy + (SIN(circuitr) * cr)
CIRCLE (v(i).x, v(i).y), 3, dotcolor
circuitr = circuitr + circuiti
NEXT
'
' Set the starting position of the fractal
'
sx = cx
sy = cy
'
' Draw the dots
'
FOR d = 1 TO maxdots
IF dotcolor <= 15 THEN
dcolor = dotcolor
ELSE
dcolor = INT(RND * 16)
END IF
CIRCLE (sx, sy), thickdots, dcolor
IF allowrepeatedEdges = 1 THEN
vi = INT(RND * edges) + 1
ELSE
pvi = vi
vi = (vi + INT(RND * (edges - 1))) MOD edges + 1
END IF
dx = v(vi).x - sx
dy = v(vi).y - sy
sx = sx + dx / wp
sy = sy + ((dy / dx) * (dx / wp))
NEXT
NEXT
My goal here is to show how to construct the Sierpinsky Triangle. The methods I used are obvious to some, but we must do justice to programmers who are just starting to learn coding and math. Derivations on how I arrived at finding the midsection of a line and other techniques I used will be discussed on separate posts.


