Lattice Paths Part 1 (Brute Force)
Starting in the top left corner of a 2 x 2 grid, and only being able to move to the right and down, there are exactly 6 routes to the bottom right corner.
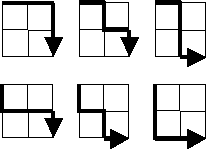
How many such routes are there through a 20 x 20 grid, or any N x N grid?
--
This is the first of a three-part series article about explaining how you could have arrived at the solution yourself in solving the Lattice Paths Problem. If you haven't tried it yet, do it first. I do not intend to deny you of your epiphany moment!
Note: All implementations are written in C/C++.
--
Brute Force
The most intuitive way to solve this problem is to think of a grid with coordinates (0, 0) at the top-left corner and (N, N) at the bottom-right corner. Then an arrowhead will traverse the grid from (0, 0) using all the combinations of Down and Right until it reaches (N, N). The number of combinations is incremented every time the arrowhead reaches (N, N). In other words, we will take a look at each possible combination of traversal.
First, we need to define a data structure where we can monitor the location of our arrowhead as it traverses the square grid. We will use this to check if the arrowhead is already on the boundary. We also need a string to monitor what has been traversed so far for each arrowhead. The string is only for debugging purposes and can be removed after we have finished the implementation of the program.
struct Coord
{
long long x, y; // X, Y
std::string combo = ""; // D-R combinations
};
Next, let's write a function and call it countRouteBruteForce() to traverse the grid with all the combinations of Down and Right from (0, 0) to (N, N). We can easily generate combinations using stacks. A step-by-step visualization for novice developers is shown below to generate the combinations of a 2 x 2 grid.
| Action | Last Pop | Stack | Count |
| push(s) | <Blank> | ||
| last = pop() | <Blank> | <Empty> | |
| push(last + "r") | r | ||
| push(last + "d") | r, d | ||
| last = pop() | d | r | |
| push(last + "r") | r, dr | ||
| push(last + "d") | r, dr, dd | ||
| last = pop() | dd | r, dr | |
| push(last + "r") | r, dr, ddr | ||
| last = pop() | ddr | r, dr | |
| push(last + "r") | r, dr, ddrr | ||
| last = pop() | ddrr | r, dr | +1 |
| last = pop() | dr | r | |
| push(last + "r") | r, drr | ||
| push(last + "d") | r, drr, drd | ||
| last = pop() | drd | r, drr | |
| push(last + "r") | r, drr, drdr | ||
| last = pop() | drdr | r, drr | +1 |
| last = pop() | drr | r | |
| push(last + "d") | r, drrd | ||
| last = pop() | drrd | r | +1 |
| last = pop() | r | <Empty> | |
| push(last + "r") | rr | ||
| push(last + "d") | rr, rd | ||
| last = pop() | rd | rr | |
| push(last + "r") | rr, rdr | ||
| push(last + "d") | rr, rdr, rdd | ||
| last = pop() | rdd | rr, rdr | |
| push(last + "r") | rr, rdr, rddr | ||
| last = pop() | rddr | rr, rdr | +1 |
| last = pop() | rdr | rr | |
| push(last + "d") | rr, rdrd | ||
| last = pop() | rdrd | rr | +1 |
| last = pop() | rr | <Empty> | |
| push(last + "d") | rrd | ||
| last = pop() | rrd | <Empty> | |
| push(last + "d") | rrdd | ||
| last = pop() | rrdd | +1 | |
| +6 |
The implementation of a stack-based determination of countRouteBruteForce function is shown below.
long long countRouteBruteForce(void)
{
std::stack <Coord>s;
Coord c;
long long count = 0;
s.push({ 0, 0, "" });
do
{
c = s.top(); s.pop();
if (c.x == MAX_SIDES && c.y == MAX_SIDES)
{
count++;
std::cout << c.combo << " (" << count << ")" << "\n";
}
else
{
// Right
if (c.x < MAX_SIDES)
s.push({ c.x + 1, c.y, c.combo + "r" });
// Down
if (c.y < MAX_SIDES)
s.push({ c.x, c.y + 1, c.combo + "d" });
}
} while (!s.empty());
return count;
}
To optimize the code, we can reduce the number of operations, remove the string, and represent the stack as an array. This will give you the following code, let's call it countRouteBruteForceArray():
long long countRouteBruteForceArray(void)
{
Coord2 s[21], c;
long long stackIdx = 0;
long long count = 0;
s[stackIdx++] = { 0, 0 };
do
{
c = s[--stackIdx];
if (c.x == MAX_SIDES && c.y == MAX_SIDES)
count++;
else
{
// Right
if (c.x < MAX_SIDES)
s[stackIdx++] = { c.x + 1, c.y };
// Down
if (c.y < MAX_SIDES)
s[stackIdx++] = { c.x, c.y + 1 };
}
} while (stackIdx > 0);
return count;
}
A recursive approach can also be written but will not be discussed here. I'll leave it up to the reader to write a recursive implementation of this function as an exercise.
The problem with a stack-based (or recursive) approach is that the generation takes some time, especially for large values of N. The table below shows how the number of combinations grow with respect to (N, N).
| No | (N, N) | N2 | Routes | No. Loops |
| 1 | 1, 1 | 1 | 2 | 5 |
| 2 | 2, 2 | 4 | 6 | 19 |
| 3 | 3, 3 | 9 | 20 | 69 |
| 4 | 4, 4 | 16 | 70 | 251 |
| 5 | 5, 5 | 25 | 252 | 923 |
| 6 | 6, 6 | 36 | 924 | 3,431 |
| 7 | 7, 7 | 49 | 3,432 | 12,869 |
| 8 | 8, 8 | 64 | 12,870 | 48,619 |
| 9 | 9, 9 | 81 | 48,620 | 184,755 |
| 10 | 10, 10 | 100 | 184,756 | 705,431 |
| 11 | 11, 11 | 121 | 705,432 | 2,704,155 |
| 12 | 12, 12 | 144 | 2,704,156 | 10,400,599 |
| 13 | 13, 13 | 169 | 10,400,600 | 40,116,599 |
| 14 | 14, 14 | 196 | 40,116,600 | 155,117,519 |
| 15 | 15, 15 | 225 | 155,117,520 | 601,080,389 |
| 16 | 16, 16 | 256 | 601,080,390 | 2,333,606,219 |
| 17 | 17, 17 | 289 | 2,333,606,220 | 9,075,135,299 |
| 18 | 18, 18 | 324 | 9,075,135,300 | 35,345,263,799 |
| 19 | 19, 19 | 361 | 35,345,263,800 | 137,846,528,819 |
| 20 | 20, 20 | 400 | 137,846,528,820 | 538,257,874,439 |
The optimized code outperforms the original function. However, it will still take even your powerful computer several hours to calculate the number of routes in a 20 x 20 grid, as the complexity in time (based on loops) is O( Routes(N+1) ) for any N x N grid (we'll uncover the nature of Routes(N) in the last part of the series). Thus, the need for another algorithm to solve this problem is necessary.
In the next aritcle (click here), you'll discover how we can reduce the time complexity of the solution to O(N2) with space complexity of O(N2).
If you're looking for the source codes, you may find it in the last part of the article (click here).


