Lattice Paths Part 2 (Brute Force Modeling and Iteration)
Starting in the top left corner of a 2 x 2 grid, and only being able to move to the right and down, there are exactly 6 routes to the bottom right corner.
How many such routes are there through a 20 x 20 grid, or any N x N grid?
--
This is the second of a three-part series article about explaining how you could have arrived at the solution yourself in solving the Lattice Paths Problem. If you haven't tried it yet, do it first. I do not intend to deny you of your epiphany moment!
Note: All implementations are written in C/C++.
--
Brute Force Modeling
After learning from the first article that Brute Force wouldn't be effective as N grows larger, we seek new methods in solving the Lattice Path Problem with a different approach. This time, let us observe how traversal combinations in a 1 x 1, 2 x 2, and 3 x 3 grids form in hopes of finding a pattern.
For the 1 x 1 grid, there are only two (2) ways you can traverse (0, 0) to (1, 1) as shown below.
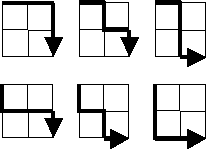
For a 2 x 2 grid, there are six (6) ways to traverse (0, 0) to (2, 2). Three (3) if you started right and another three (3) if you started down.
Now, this next step is important. For the arrowhead that started from the right, let's breakdown the ways by the first time it turned down by column. Let's do the same for the arrowhead that started down, but break it down by the first time it turned right by row.
This categorization of total combination by the first turn per column or row is shown in the figure below.
Let's do a similar categorization for the 3 x 3 grid.
Let's perform a Brute Force Modeling by stacking up our data for each grid size in a table and see how these three (3) sets of data relate to each other.
| Started Right | Started Down | Combinations | |||||||||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 0 | 1 | 2 | 3 | 4 | 5 | ||||||||
| 1x1 | 1 | 1 | 1 | 1 | 2 | ||||||||||||||
| 2x2 | 2 | 1 | 2 | 2 | 1 | 2 | 6 | ||||||||||||
| 3x3 | 3 | 1 | 3 | 6 | 3 | 1 | 3 | 6 | 20 | ||||||||||
From the data, we can observe the following:
- The first column is always one (1), this makes sense regardless of the matrix because you only turn down once from the farthest right. And you only turn right once if you're in the most bottom part of the matrix.
- The second column is always equal to N, as we can inductively conclude this from the diagrams above.
- The Nth column of the set is equal to the sum of all columns of the previous set multiplied by two (2). i.e. 6 = (1+ 2) x 2; 2 = (1) x 2
- The Nth - 1 column of the set is equal to the sum of all columns of the previous set. i.e. 3 = (1 + 2)
- The combination is the total of the N x N matrix for both columns of the Started Right and Started Down tables.
Let's complete the set for 4x4 and 5x5 grids using our observation, thus we get:
| Started Right | + | Started Down | Combinations | |||||||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 0 | 1 | 2 | 3 | 4 | 5 | |||||||
| 1x1 | 1 | 1 | 1 | 1 | 2 | |||||||||||||
| 2x2 | 2 | 1 | 2 | 2 | 1 | 2 | 6 | |||||||||||
| 3x3 | 3 | 1 | 3 | 6 | 3 | 1 | 3 | 6 | 20 | |||||||||
| 4x4 | 4 | 1 | 4 | 10 | 20 | 4 | 1 | 4 | 10 | 20 | 70 | |||||||
| 5x5 | 5 | 1 | 5 | 15 | 35 | 70 | 5 | 1 | 5 | 15 | 35 | 70 | 252 | |||||
By another close inspection, we can simplify the computation if
- We populate the blank columns with the field adjacent to their lower left.
- To compute for any column in the table between (2, 2) to (N, N), one has to add the cell on the left and the cell on top. As these cells represent the observation we previously had.
- Since Started Right Table is just a duplicate of Started Down Table, we can discard one of the tables and just multiply the total of all the columns by two (2) of a particular set to get the number of combinations. The table below describes this new observation.
| Table | Combinations | |||||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | |||||||||
| 1x1 | 1 | 1 | 1 | 1 | 1 | 1 | 2 | |||||||
| 2x2 | 2 | 1 | 2 | 3 | 4 | 5 | 6 | |||||||
| 3x3 | 3 | 1 | 3 | 6 | 10 | 15 | 20 | |||||||
| 4x4 | 4 | 1 | 4 | 10 | 20 | 35 | 70 | |||||||
| 5x5 | 5 | 1 | 5 | 15 | 35 | 70 | 252 | |||||||
Our new observation can be written in countRouteTabulation() function below:
long long countRouteTabulation(void)
{
long long total;
long long routes[MAX_SIDES][MAX_SIDES];
int x, y;
for (x = 0; x < MAX_SIDES; x++)
{
routes[0][x] = 1;
routes[x][0] = 1;
}
for (y = 1; y < MAX_SIDES; y++)
for (x = 1; x < MAX_SIDES; x++)
routes[y][x] = routes[y - 1][x] + routes[y][x - 1];
for (total = 0, y = MAX_SIDES - 1, x = 0; x < MAX_SIDES; x++)
total += routes[y][x];
return total * 2;
}
Finally, we can optimize the code by these new observations:
- We can start with 2 instead of 1 so we don't have to multiply by 2
- We can add a column in the routes array so we can remove the last for-loop as the last column and row will give us the number of combinations we are looking for.
Our final observations yield the following table of a 4 x 4 grid.
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 2 | 2 | 2 | 2 | 2 |
| 2 | 2 | 4 | 6 | 8 | 10 |
| 3 | 2 | 6 | 12 | 20 | 30 |
| 4 | 2 | 8 | 20 | 40 | 70 |
Our final observation can be written as countRouteTabulationOptim() below:
long long countRouteTabulationOptim(void)
{
long long total;
long long routes[MAX_SIDES][MAX_SIDES + 1];
int x, y;
for (x = 0; x < MAX_SIDES; x++)
{
routes[0][x] = 2;
routes[x][0] = 2;
} routes[0][x] = 2;
for (y = 1; y < MAX_SIDES; y++)
for (x = 1; x <= MAX_SIDES; x++)
routes[y][x] = routes[y - 1][x] + routes[y][x - 1];
return routes[MAX_SIDES - 1][MAX_SIDES];
}
This program gives us O(N2) Time and Space Complexity for any N x N grid. A lot better compared to the Brute Force approach. The reader might be amused to try and find out a recursive and memoization approach with the same time and space complexity as the code above.
As we all know, solutions with O(N2) Complexity should be avoided if better solutions exist. It turned out that there's another way to solve this problem in O(N) Time Complexity with O(1) Space Complexity. This approach will be discussed in the next part (click here). Source codes can also be found on the same link.


